Aplicación de las operaciones con conjuntos

Las operaciones básicas del álgebra de conjuntos son:
  • Unión. La unión de dos conjuntos A y B es el conjunto A ∪ B que contiene todos los elementos de A y de B.
  • Intersección. La intersección de dos conjuntos A y B es el conjunto A ∩ B que contiene todos los elementos comunes de A y B.
  • Diferencia. La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.
  • Diferencia simétrica. La diferencia simétrica entre dos conjuntos A y B es el conjunto que contiene los elementos de A y B que no son comunes.
  • Complemento. El complemento de un conjunto A es el conjunto A∁ que contiene todos los elementos que no pertenecen a A.
  • Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B que contiene todos los pares ordenados (a, b) cuyo primer elemento pertenece a A y su segundo elemento pertenece a B.

Unión de conjuntos

Supongamos que tenemos los conjuntos  y  definidos como se muestra en la siguiente figura:
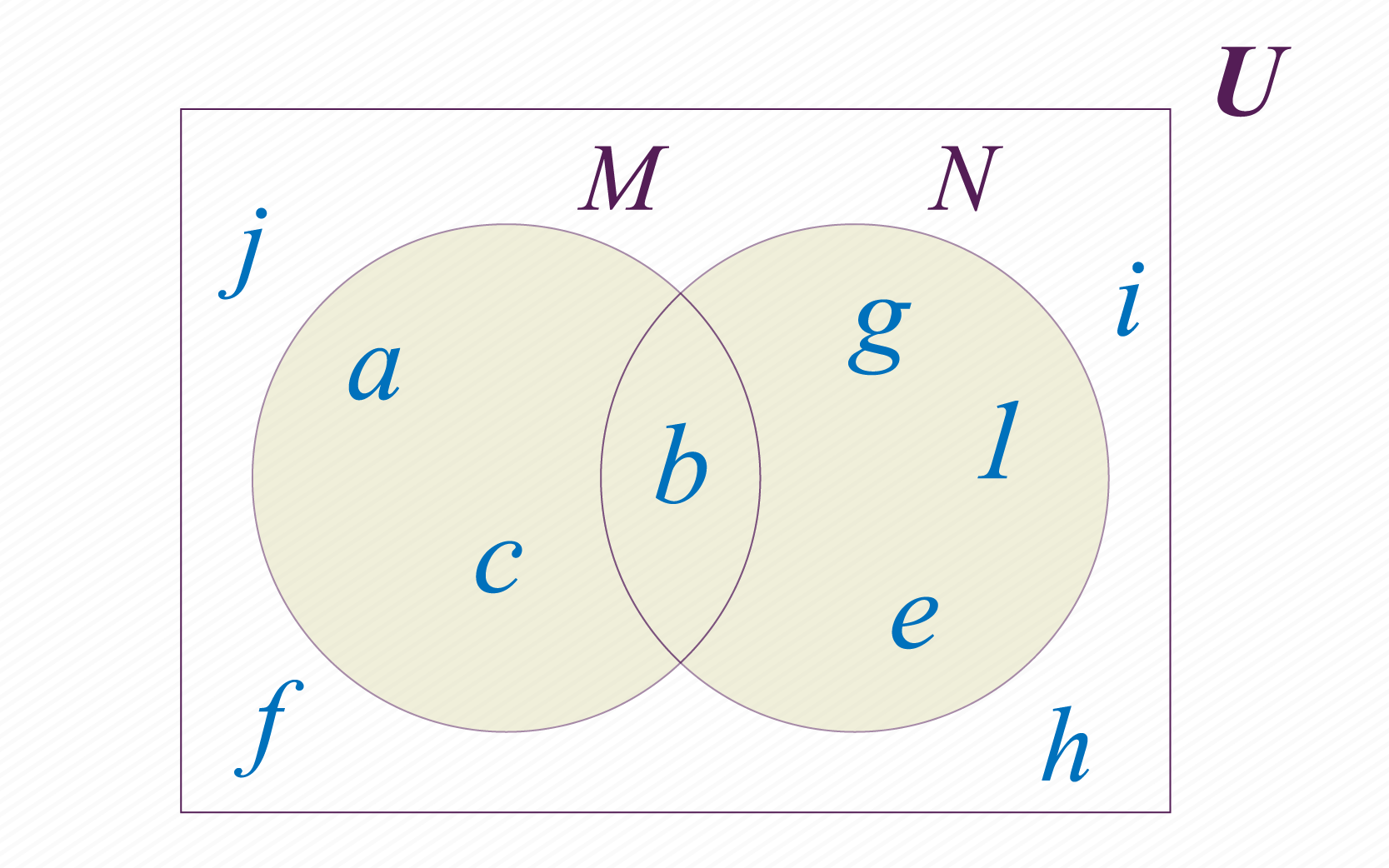
Conjuntos M y N.
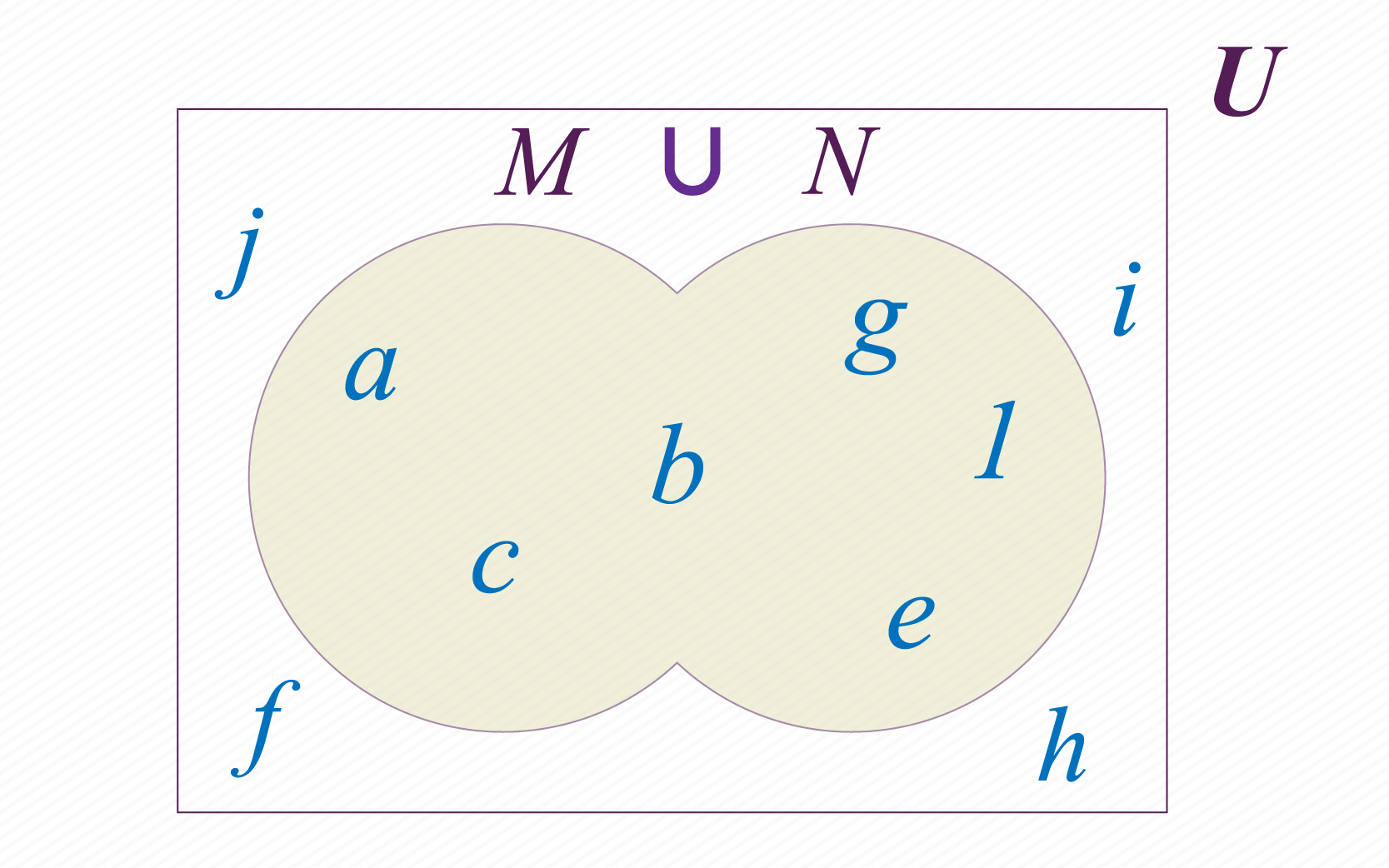
Podemos crear otro conjunto conformado con los elementos que pertenezcan a  o a .  A este nuevo conjunto le llamamos unión de  y , y lo notamos de la siguiente manera: .  En la imagen de abajo puedes observar el resultado de unir los conjuntos  y .
Al elegir qué elementos estarán en la unión de nuestros conjuntos  y , debes preguntarte cuáles están en el conjunto  “o” en el conjunto .  El resultado de la operación será el conjunto conformado por todos los elementos del conjunto universal , que cumplan la condición de estar en uno o en otro.
Tenemos en este caso: :
Unión de M y N.

Intersección de conjuntos

Sigamos tomando como ejemplo los conjuntos  y  definidos anteriormente.  Podemos determinar un nuevo conjunto conformado por los elementos que nuestros conjuntos  y  tienen en común.  A este nuevo conjunto le llamamos intersección de  y , y lo notamos de la siguiente manera: .
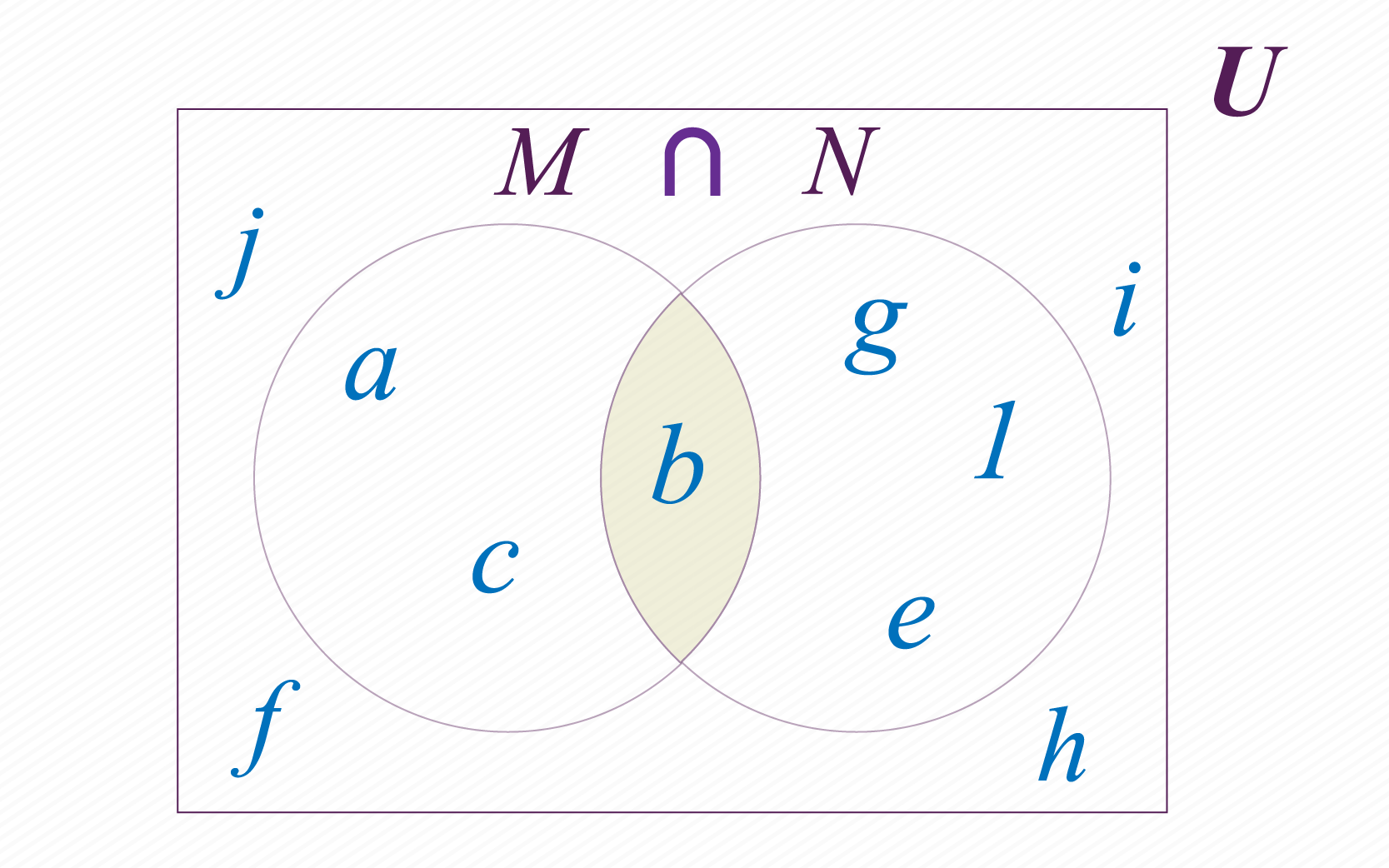
Intersección de M y N.
Para determinar que elementos pertenecen a la intersección de los conjuntos  y  te puedes preguntar qué elementos están en  “y” en   Todos los elementos del conjunto  que cumplan esta condición deberán estar en el conjunto .  En la figura de la arriba puedes ver la intersección de nuestros conjuntos  y : .

Diferencia de conjuntos

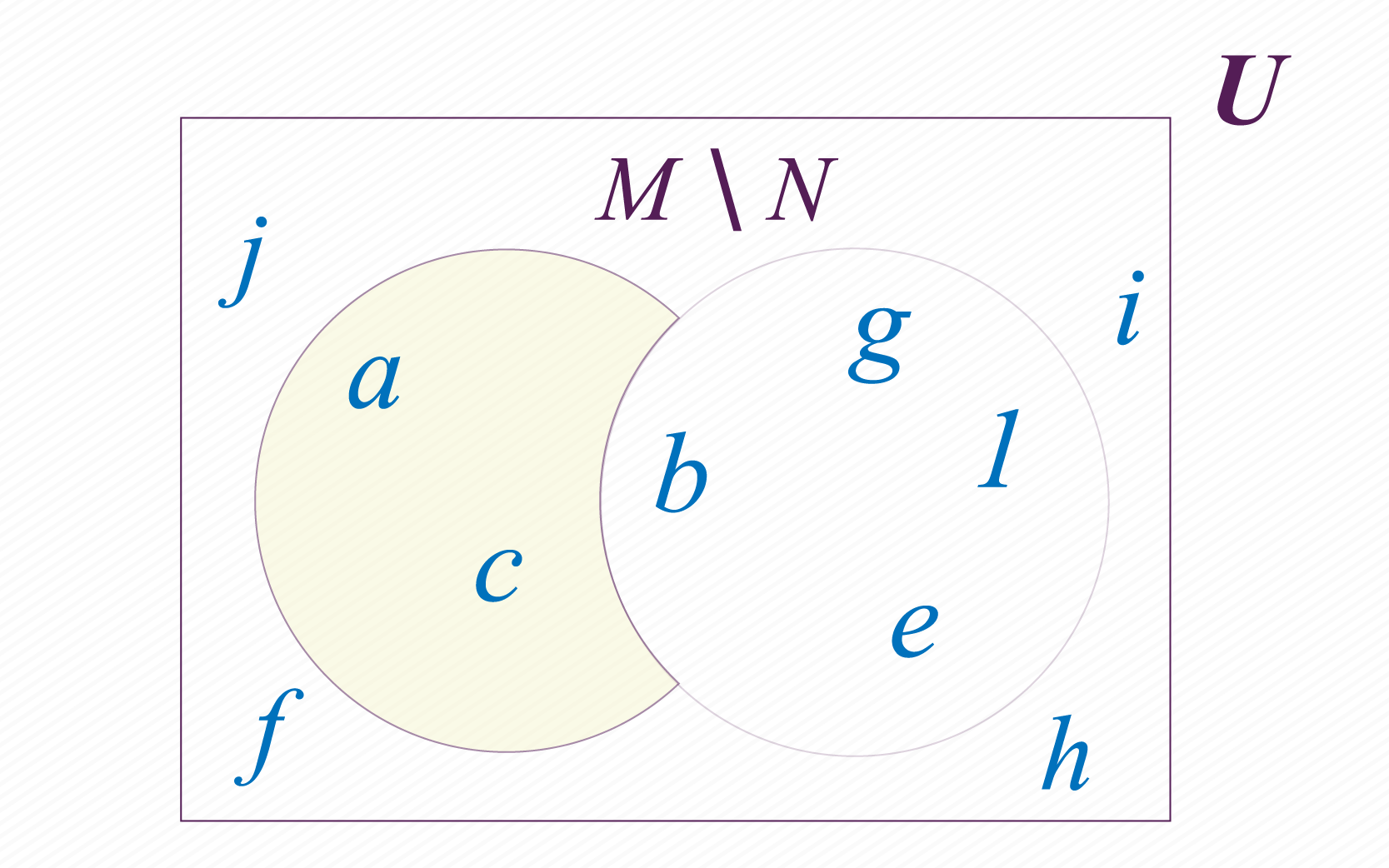
Además de la unión y la intersección podemos realizar la diferencia de conjuntos.
En este caso se deben seleccionar los elementos de un conjunto que no estén en el otro.  Por ejemplo, si realizas la operación menos , debes seleccionar los elementos de  que no están en .  Representamos la diferencia M menos N así: .  Observa que en este caso .
Diferencia M menos N.

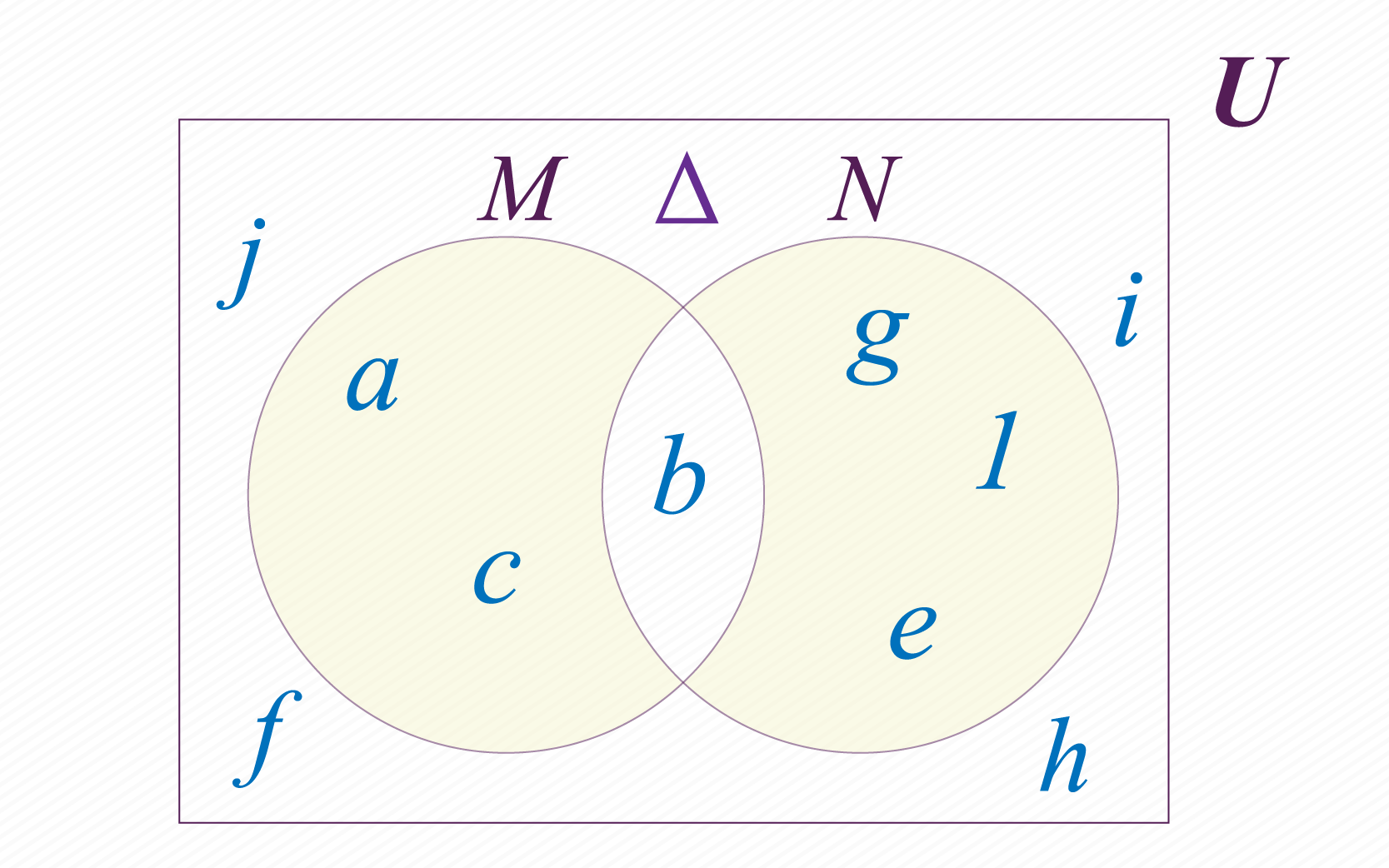
Diferencia simétrica de conjuntos

Que el nombre esta operación no te alarme, también es muy sencilla.
En esta ocasión se deben escoger los elementos de  que no están en , y los elementos de  que no están en .  Puedes ver el resultado de la diferencia simétrica entre  y  en la figura de abajo.  Representamos la diferencia simétrica a través del símbolo .  En el caso de nuestros conjuntos  y  tenemos: .

Diferencia simétrica entre M y N.

Complemento de un conjunto

La ultima operación que estudiaremos no es entre dos conjuntos.  Decimos que el complemento de  es el conjunto conformado por todos los elementos del conjunto universal , que no pertenecen al conjunto .  Es común usar los símbolos ,  o  para representar el complemento del conjunto . Nosotros usaremos el símbolo .  En nuestro caso tenemos  y .
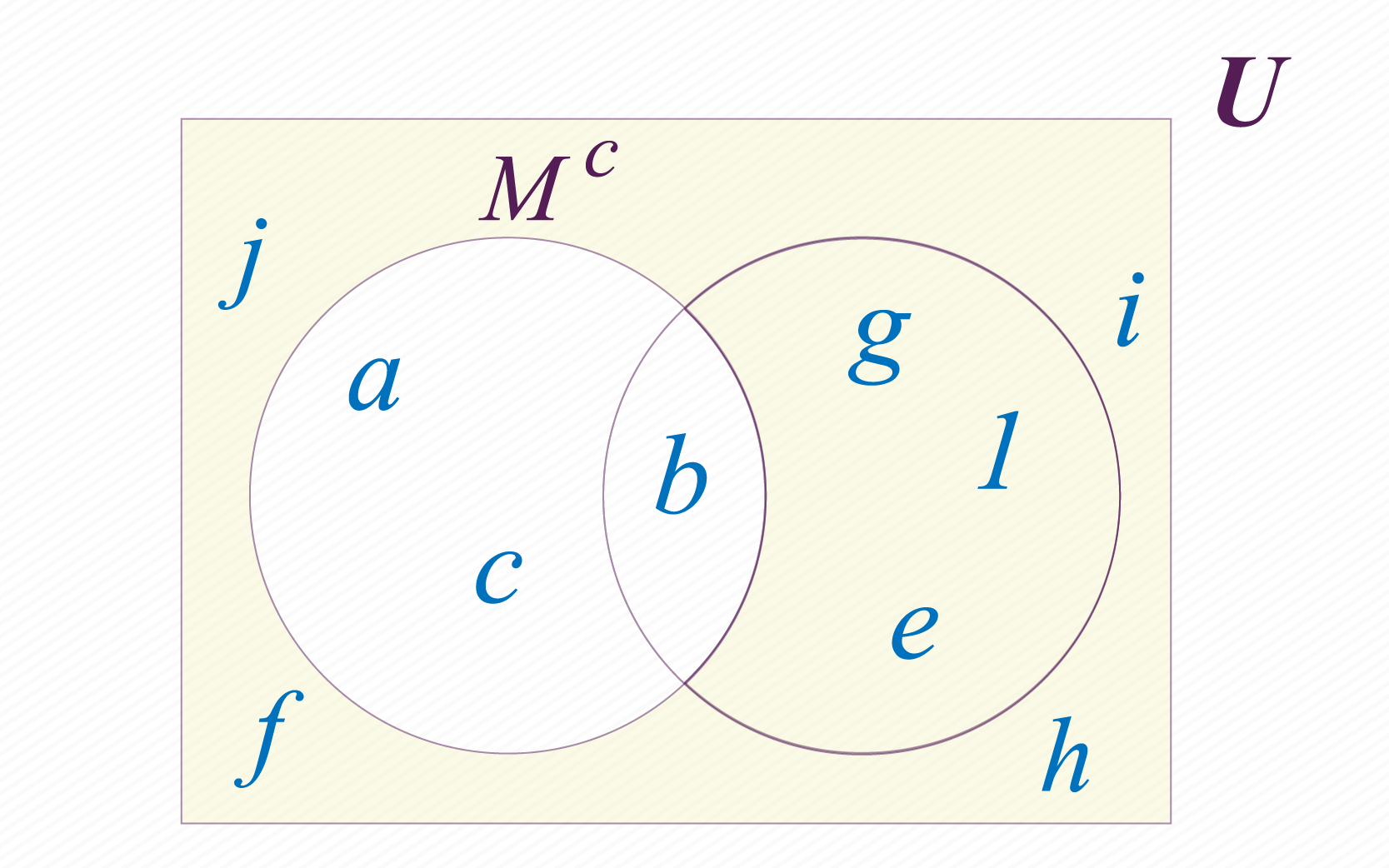
Complemento del conjunto M.

Comentarios

Publicar un comentario

Entradas más populares de este blog

Resolver un Problema Similar más Sencillo

Imagen
Como lo dice el nombre de la estrategia, este método consiste en buscar un problema que tenga las mismas bases, solo que este sea mas sencillo que nuestro problema anterior, y de esta manera relacionarlos entre sí y cumplir con nuestro objetivo que es darle solución a nuestro problema original. Opinión La estrategia de resolver un problema similar más simple me gusta a pesar de no ser la que más se me facilita, pues es difícil encontrarle lógica para llegar a la solución. Ejemplo: Usted tiene ocho monedas y una es falsa, por ello pesa menos que las demás. También tiene una balanza con platillos que puede usar solamente tres veces. Diga cómo descubrir la moneda falsa en tres pesajes. Luego, muestre cómo detectar la moneda falsa únicamente con dos pesajes. Para llegar a la solución de una forma más sencilla, decidimos aplicar los cuatro pasos de Polya. 1. Determinar la moneda falsa 1 con 1 pesaje y luego con 2. 2. Se utilizará la estrategia de Resolver un Problema Similar...
Leer más

Ensayo y Error

Imagen
La ciencia busca la verdad. El método científico se basa en la razón, en pruebas, en datos, etc. Dejando a un lado las matemáticas, ciencia exacta que se construye a sí misma, el resto de ciencias se basan en la observación, en lo empírico. Crear leyes y teorías es la manera de estructurar el comportamiento de la naturaleza, sin incongruencias, sin contradicciones. Es por ello que se dice que la ciencia se basa en la técnica ensayo y error. El ensayo y error es la técnica de aprendizaje más extendida y natural. Un niño aprende a que el fuego es una energía exotérmica intensa cuando se quema, un adulto aprende a que un modelo económico no es estable cuando su inversión produce una quiebra, y así todos nos basamos en la observación para crear un pensamiento crítico. En particular, el arte se basa en la intuición, que se puede percibir como algo mágico pero nace de patrones recurrentes que generamos por nuestro mundo observado, y también el conocimiento y por supuesto en el 'ensay...
Leer más